殊途同归:求解50阶导数
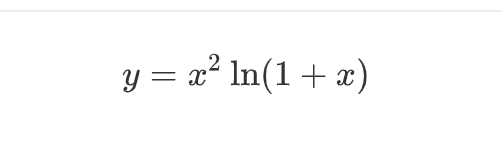
殊途同归:求解50阶导数
Wang YinXi殊途同归:求解
$$ y = x^2 \ln(1+x) $$的50阶导数
在数学中,高阶导数的计算往往充满挑战,但也展示了不同方法的巧妙之处。本文将以函数
$$
y = x^2 \ln(1+x)
$$
为例,探讨两种截然不同的路径来求解其50阶导数
$$
y^{(50)}
$$
,并证明它们最终殊途同归。
问题介绍
考虑函数
$$
y = x^2 \ln(1+x)
$$
我们的目标是计算其50阶导数
$$
y^{(50)}
$$
直接逐阶求导显然不现实,因此需要更高效的方法。下面将展示两种路径:一是使用莱布尼茨公式(基于乘积法则的推广),二是从低阶导数的模式识别出发,建立递推关系。
路径一:莱布尼茨公式法
莱布尼茨公式是计算两个函数乘积的高阶导数的强大工具。对于函数
$$
y = u(x) v(x)
$$
,有:
$$
(uv)^{(n)} = \sum_{k=0}^{n} \binom{n}{k} u^{(k)} v^{(n-k)}
$$
在本例中,令
$$
u(x) = x^2 \quad \text{和} \quad v(x) = \ln(1+x)
$$
已知导数
- $$ u(x) = x^2,因此: u' = 2x, \quad u'' = 2, \quad u^{(k)} = 0 \quad \text{for} \quad k \geq 3 $$
-
$$
v(x) = \ln(1+x)
$$
,其高阶导数为:
$$ v^{(m)} = (-1)^{m-1} \frac{(m-1)!}{(1+x)^m} \quad \text{for} \quad m \geq 1 $$
应用莱布尼茨公式
由于
$$
u^{(k)} = 0
$$
对于
$$
k \geq 3
$$
,莱布尼茨公式简化为:
$$
y^{(n)} = \binom{n}{0} u v^{(n)} + \binom{n}{1} u' v^{(n-1)} + \binom{n}{2} u'' v^{(n-2)}
$$
代入表达式:
$$
y^{(n)} = x^2 v^{(n)} + n \cdot 2x \cdot v^{(n-1)} + \frac{n(n-1)}{2} \cdot 2 \cdot v^{(n-2)} = x^2 v^{(n)} + 2n x v^{(n-1)} + n(n-1) v^{(n-2)}
$$
计算
$$ y^{(50)} $$对于
$$
n = 50
$$
,需要:
$$
v^{(50)} = (-1)^{49} \frac{49!}{(1+x)^{50}} = -\frac{49!}{(1+x)^{50}}
$$
代入公式:
$$
y^{(50)} = x^2 \left( -\frac{49!}{(1+x)^{50}} \right) + 2 \cdot 50 \cdot x \cdot \left( \frac{48!}{(1+x)^{49}} \right) + 50 \cdot 49 \cdot \left( -\frac{47!}{(1+x)^{48}} \right)
$$
简化:
$$
y^{(50)} = -\frac{49! x^2}{(1+x)^{50}} + \frac{100 \cdot 48! x}{(1+x)^{49}} - \frac{2450 \cdot 47!}{(1+x)^{48}}
$$
路径二:模式识别与递推法
另一种方法是从低阶导数中观察模式,并建立递推关系。计算前几阶导数:
一阶导数:
$$ y' = 2x \ln(1+x) + \frac{x^2}{x+1} $$二阶导数:
$$ y'' = 2 \ln(1+x) + \frac{2x}{x+1} + 1 - \frac{1}{(x+1)^2} $$三阶导数:
$$ y''' = \frac{2}{x+1} + \frac{2}{(x+1)^2} + \frac{2}{(x+1)^3} $$
从三阶导数开始,可以看到一个清晰的模式:
$$
y^{(n)}
$$
可以表示为若干分式的和,其分母为
$$
(1+x)^k
$$
,其中 k 从 n-2 到 n。
建立递推关系
假设对于
$$
n \geq 3
$$
,有:
$$
y^{(n)} = \sum_{k=n-2}^{n} \frac{c_{n,k}}{(1+x)^k}
$$
从三阶导数知:
$$
c_{3,1} = 2, c_{3,2} = 2, c_{3,3} = 2
$$
每次求导时,项
$$
\frac{c}{(1+x)^k}
$$
变为
$$
\frac{-k c}{(1+x)^{k+1}}
$$
,因此系数递推关系为:
$$
c_{n+1,k} = - (k-1) c_{n,k-1}
$$
通过递推,可以导出一般公式:
$$
c_{n,k} = (-1)^{n-3} \cdot 2 \cdot \frac{(k-1)!}{(k-n+2)!} \quad \text{for} \quad k = n-2, n-1, n
$$
计算
$$ y^{(50)} $$对于 n = 50,有 (-1)^{50-3} = (-1)^{47} = -1,因此:
$$
k = 48: c_{50,48} = -2 \cdot \frac{47!}{(48-50+2)!} = -2 \cdot \frac{47!}{0!} = -2 \cdot 47!
$$
所以:
$$
y^{(50)} = \frac{c_{50,48}}{(1+x)^{48}} + \frac{c_{50,49}}{(1+x)^{49}} + \frac{c_{50,50}}{(1+x)^{50}} = -\frac{2 \cdot 47!}{(1+x)^{48}} - \frac{2 \cdot 48!}{(1+x)^{49}} - \frac{49!}{(1+x)^{50}}
$$
比较与验证
现在,我们有两个表达式:
来自莱布尼茨公式:
$$ y^{(50)} = -\frac{49! x^2}{(1+x)^{50}} + \frac{100 \cdot 48! x}{(1+x)^{49}} - \frac{2450 \cdot 47!}{(1+x)^{48}} $$来自模式识别:
$$ y^{(50)} = -\frac{2 \cdot 47!}{(1+x)^{48}} - \frac{2 \cdot 48!}{(1+x)^{49}} - \frac{49!}{(1+x)^{50}} $$
为了比较,将莱布尼茨公式的结果通分到分母 $(1+x)^{50}$:
$$
y^{(50)} = \frac{ -49! x^2 + 100 \cdot 48! x (1+x) - 2450 \cdot 47! (1+x)^2 }{(1+x)^{50}}
$$
代入
$$
48! = 48 \cdot 47! \quad \text{和} \quad 49! = 49 \cdot 48 \cdot 47!
$$
,分子变为:
$$
47! \left[ -49 \cdot 48 x^2 + 100 \cdot 48 x (1+x) - 2450 (1 + 2x + x^2) \right] = 47! (-2x^2 -100x -2450)
$$
所以:
$$
y^{(50)} = \frac{ 47! (-2x^2 -100x -2450) }{(1+x)^{50}}
$$
将模式识别结果通分:
$$
y^{(50)} = \frac{ -2 \cdot 47! (1+x)^2 - 2 \cdot 48! (1+x) - 49! }{(1+x)^{50}}
$$
代入
$$
48! = 48 \cdot 47! \quad \text{和} \quad 49! = 49 \cdot 48 \cdot 47!
$$
,分子变为:
$$
47! \left[ -2 (1+x)^2 - 2 \cdot 48 (1+x) - 49 \cdot 48 \right] = 47! (-2x^2 -100x -2450)
$$
因此,两个表达式完全相同,验证了它们殊途同归。
结论
通过莱布尼茨公式和模式识别两种路径,我们得到了相同的50阶导数表达式。这不仅展示了数学工具的威力,也体现了数学内在的一致性。在实际应用中,根据具体情况选择合适的方法可以大大简化计算。
数学的魅力在于,无论从何处开始,最终都能到达真理的彼岸。